The shot angle of the ball is determined by the angle of the face (note that the swing path has nothing to do with the shot angle).
So how many degrees off the target line does it take to cause a shift in distance on the side?
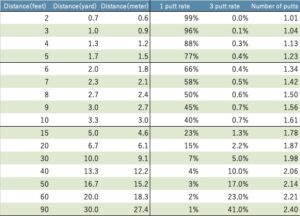
Here’s a list of how much you can shift to the side by distance.
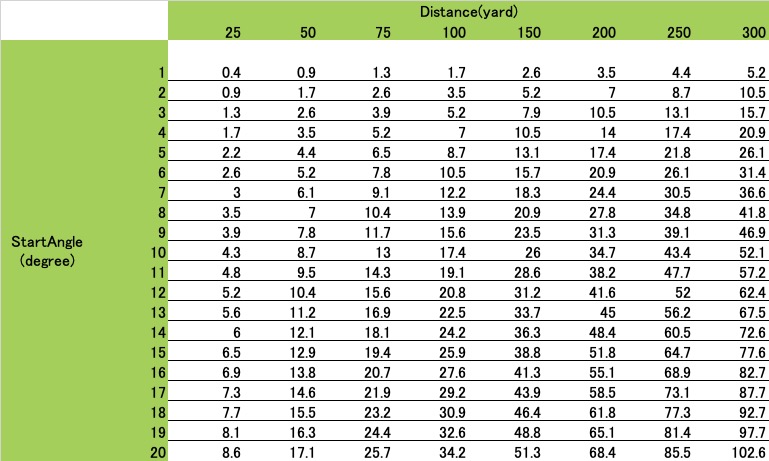
At a distance of 100 yards, a 10-degree misalignment of the face from the target direction will result in a 13-yard lateral misalignment from the pin, ignoring side spin due to misalignment of the swing path.
At a distance of 250 yards, a 10-degree deviation of the face from the target would result in a lateral deviation of 43.4 yards from the target.
Of course, the longer the distance, the greater the misalignment of the launch angle.
For example, at a distance of 100 yards, a 10-degree misalignment of the face of the ball by 13 yards is not a big problem, but a 43.4 yard misalignment on the tee shot is fatal because of the high risk of OB.
Also, by measuring the lateral distance error, you will be able to tell how many degrees the face is open or closed.
This will give you an idea of how much you need to close or open the face on your next shot.
Incidentally, it is relatively easy to find this error using trigonometric functions.
In business, it is often easy to find the answer by using mathematics invented by our great ancestors, but I feel that it is just social damage that there are many businessmen who do not want to use mathematics or cannot use it.
Here’s how to calculate the side error. There is no problem to skip reading.
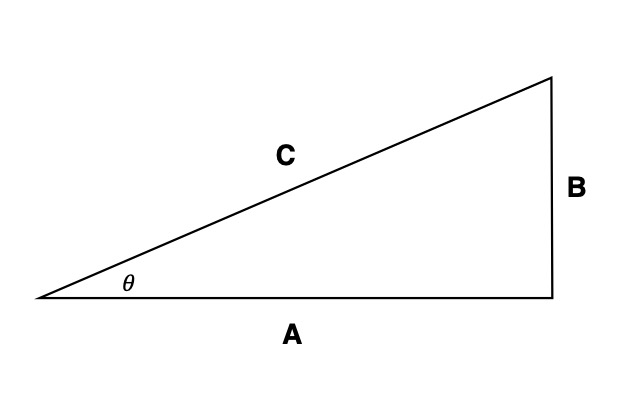
Consider a triangle like this
例えば、Xというゴルファーが100ヤード真っ直ぐ飛ばせるとします。
この三角形なら、Aの辺が100ヤードとします。
で、Cの辺の長さを求めれば良いと一瞬思うかもしれませんが、それでは正確ではありません。
Xの飛距離は250ヤードなので、C方向に打ち出されたボールの飛距離も100ヤードであるべきです(打ち出し方向によって飛距離が変わると言うゴルファーもいると思いますが、この場合は無視します。ちなみに、右に打ち出そうが、左に打ち出そうが、多くのゴルファーは実際のところ、そんなに飛距離は変わらないと思います)。
また、シンプルにするためサイドスピンも考慮しません。
実際のCの辺の長さはAよりも長いので、Bのサイドの誤差は実際よりも大きくなってしまいます。
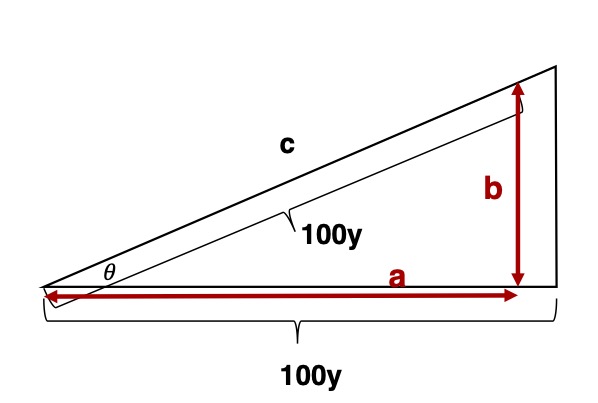
なので、XがC方向に100ヤード飛ばした時の三角形の高さを求めなればなりません。
それは、まず、XがC方向に打ち出した時の、直線距離aを求めて、その後、直線距離aからの三角形の高さbを求めます。
For example, let’s say a golfer named X can fly 100 yards straight.
In this triangle, let’s say that the side of A is 100 yards.
You may think for a moment that you can just find the length of the side C, but that is not accurate.
The distance of X is 250 yards, so the distance of the ball launched in the direction of C should also be 100 yards (I know some golfers say that the distance changes depending on the direction of launch, but in this case I will ignore it. Some golfers may say that the distance changes depending on the direction of launch, but in this case, I will ignore it, because most golfers don’t really care whether they launch the ball to the right or to the left.)
Also, for simplicity’s sake, I don’t take into account side spin.
Since the actual length of the side of C is longer than that of A, the error on the side of B will be larger than it actually is.
So, we need to find the height of the triangle when X flies 100 yards in the direction of C.
To do this, first find the straight line distance a when X launches in the direction of C, and then find the height of the triangle b from the straight line distance a.
It can be obtained by using this formula.
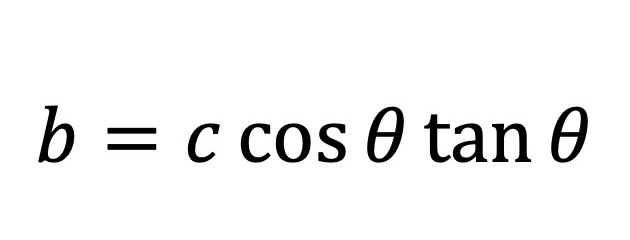
It can also be easily calculated in Excel.
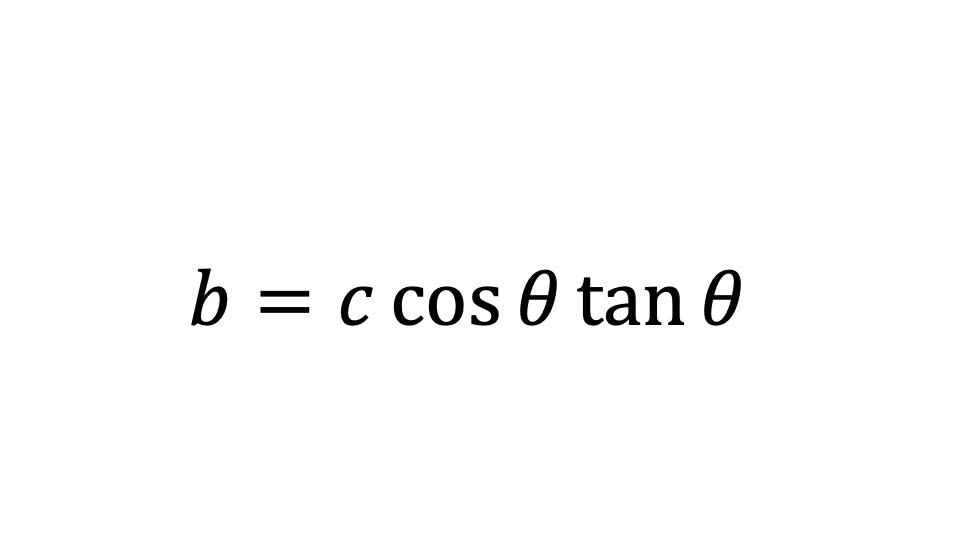
Comments